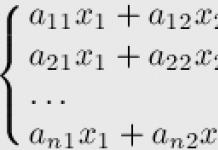Метод гаусса как сделать проверку. Метод Гаусса (последовательного исключения неизвестных)

Дана система линейных алгебраических уравнений (СЛАУ) с неизвестными. Требуется решить эту систему: определить, сколько решений она имеет (ни одного, одно или бесконечно много), а если она имеет хотя бы одно решение, то найти любое из них.

Формально задача ставится следующим образом: решить систему:

где коэффициенты и известны, а переменные — искомые неизвестные.

Удобно матричное представление этой задачи:

где — матрица , составленная из коэффициентов , и — векторы-столбцы высоты .

Стоит отметить, что СЛАУ может быть не над полем действительных чисел, а над полем по модулю какого-либо числа , т.е.:

— алгоритм Гаусса работает и для таких систем тоже (но этот случай будет рассмотрен ниже в отдельном разделе).

Алгоритм Гаусса

Строго говоря, описываемый ниже метод правильно называть методом "Гаусса-Жордана" (Gauss-Jordan elimination), поскольку он является вариацией метода Гаусса, описанной геодезистом Вильгельмом Жорданом в 1887 г. (стоит отметить, что Вильгельм Жордан не является автором ни теоремы Жордана о кривых, ни жордановой алгебры — всё это три разных учёных-однофамильца; кроме того, по всей видимости, более правильной является транскрипция "Йордан", но написание "Жордан" уже закрепилось в русской литературе). Также интересно заметить, что одновременно с Жорданом (а по некоторым данным даже раньше него) этот алгоритм придумал Класен (B.-I. Clasen).

Базовая схема

Кратко говоря, алгоритм заключается в последовательном исключении переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется только по одной переменной. Если , то можно говорить, что алгоритм Гаусса-Жордана стремится привести матрицу системы к единичной матрице — ведь после того как матрица стала единичной, решение системы очевидно — решение единственно и задаётся получившимися коэффициентами .

При этом алгоритм основывается на двух простых эквивалентных преобразованиях системы: во-первых, можно обменивать два уравнения, а во-вторых, любое уравнение можно заменить линейной комбинацией этой строки (с ненулевым коэффициентом) и других строк (с произвольными коэффициентами).

На первом шаге алгоритм Гаусса-Жордана делит первую строку на коэффициент . Затем алгоритм прибавляет первую строку к остальным строкам с такими коэффициентами, чтобы их коэффициенты в первом столбце обращались в нули — для этого, очевидно, при прибавлении первой строки к -ой надо домножать её на . При каждой операции с матрицей (деление на число, прибавление к одной строке другой) соответствующие операции производятся и с вектором ; в некотором смысле, он ведёт себя, как если бы он был -ым столбцом матрицы .

В итоге, по окончании первого шага первый столбец матрицы станет единичным (т.е. будет содержать единицу в первой строке и нули в остальных).

Аналогично производится второй шаг алгоритма, только теперь рассматривается второй столбец и вторая строка: сначала вторая строка делится на , а затем отнимается от всех остальных строк с такими коэффициентами, чтобы обнулять второй столбец матрицы .

Поиск опорного элемента (pivoting)

Разумеется, описанная выше схема неполна. Она работает только в том случае, если на каждом -ом шаге элемент отличен от нуля — иначе мы просто не сможем добиться обнуления остальных коэффициентов в текущем столбце путём прибавления к ним -ой строки.

Чтобы сделать алгоритм работающим в таких случаях, как раз и существует процесс выбора опорного элемента (на английском языке это называется одним словом "pivoting"). Он заключается в том, что производится перестановка строк и/или столбцов матрицы, чтобы в нужном элементе оказалось ненулевое число.

Заметим, что перестановка строк значительно проще реализуется на компьютере, чем перестановка столбцов: ведь при обмене местами двух каких-то столбцов надо запомнить, что эти две переменных обменялись местами, чтобы затем, при восстановлении ответа, правильно восстановить, какой ответ к какой переменной относится. При перестановке строк никаких таких дополнительных действий производить не надо.

К счастью, для корректности метода достаточно одних только обменов строк (т.н. "partial pivoting", в отличие от "full pivoting", когда обмениваются и строки, и столбцы). Но какую же именно строку следует выбирать для обмена? И правда ли, что поиск опорного элемента надо делать только тогда, когда текущий элемент нулевой?

Общего ответа на этот вопрос не существует. Есть разнообразные эвристики, однако самой эффективной из них (по соотношению простоты и отдачи) является такая эвристика : в качестве опорного элемента следует брать наибольший по модулю элемент, причём производить поиск опорного элемента и обмен с ним надо всегда , а не только когда это необходимо (т.е. не только тогда, когда ).

Иными словами, перед выполнением -ой фазы алгоритма Гаусса-Жордана с эвристикой partial pivoting необходимо найти в -ом столбце среди элементов с индексами от до максимальный по модулю, и обменять строку с этим элементом с -ой строкой.

Во-первых, эта эвристика позволит решить СЛАУ, даже если по ходу решения будет случаться так, что элемент . Во-вторых, что весьма немаловажно, эта эвристика улучшает численную устойчивость алгоритма Гаусса-Жордана.

Без этой эвристики, даже если система такова, что на каждой -ой фазе — алгоритм Гаусса-Жордана отработает, но в итоге накапливающаяся погрешность может оказаться настолько огромной, что даже для матриц размера около погрешность будет превосходить сам ответ.

Вырожденные случаи

Итак, если останавливаться на алгоритме Гаусса-Жордана с partial pivoting, то, утверждается, если и система невырождена (т.е. имеет ненулевой определитель, что означает, что она имеет единственное решение), то описанный выше алгоритм полностью отработает и придёт к единичной матрице (доказательство этого, т.е. того, что ненулевой опорный элемент всегда будет находиться, здесь не приводится).

Рассмотрим теперь общий случай — когда и не обязательно равны. Предположим, что опорный элемент на -ом шаге не нашёлся. Это означает, что в -ом столбце все строки, начиная с текущей, содержат нули. Утверждается, что в этом случае эта -ая переменная не может быть определена, и является независимой переменной (может принимать произвольное значение). Чтобы алгоритм Гаусса-Жордана продолжил свою работу для всех последующих переменных, в такой ситуации надо просто пропустить текущий -ый столбец, не увеличивая при этом номер текущей строки (можно сказать, что мы виртуально удаляем -ый столбец матрицы).

Итак, некоторые переменные в процессе работы алгоритма могут оказываться независимыми. Понятно, что когда количество переменных больше количества уравнений, то как минимум переменных обнаружатся независимыми.

В целом, если обнаружилась хотя бы одна независимая переменная, то она может принимать произвольное значение, в то время как остальные (зависимые) переменные будут выражаться через неё. Это означает, что, когда мы работаем в поле действительных чисел, система потенциально имеет бесконечно много решений (если мы рассматриваем СЛАУ по модулю, то число решений будет равно этому модулю в степени количества независимых переменных). Впрочем, следует быть аккуратным: надо помнить о том, что даже если были обнаружены независимые переменные, тем не менее СЛАУ может не иметь решений вовсе . Это происходит, когда в оставшихся необработанными уравнениях (тех, до которых алгоритм Гаусса-Жордана не дошёл, т.е. это уравнения, в которых остались только независимые переменные) есть хотя бы один ненулевой свободный член.

Впрочем, проще это проверить явной подстановкой найденного решения: всем независимыми переменным присвоить нулевые значения, зависимым переменным присвоить найденные значения, и подставить это решение в текущую СЛАУ.

Реализация

Приведём здесь реализацию алгоритма Гаусса-Жордана с эвристикой partial pivoting (выбором опорного элемента как максимума по столбцу).

На вход функции передаётся сама матрица системы . Последний столбец матрицы — это в наших старых обозначениях столбец свободных коэффициентов (так сделано для удобства программирования — т.к. в самом алгоритме все операции со свободными коэффициентами повторяют операции с матрицей ).

Функция возвращает число решений системы (, или ) (бесконечность обозначена в коде специальной константой , которой можно задать любое большое значение). Если хотя бы одно решение существует, то оно возвращается в векторе .

int gauss (vector < vector< double > > a, vector< double > & ans) { int n = (int ) a.size () ; int m = (int ) a[ 0 ] .size () - 1 ; vector< int >< m && row< n; ++ col) { int sel = row; for (int i= row; i< n; ++ i) if (abs (a[ i] [ col] ) > abs (a[ sel] [ col] ) ) sel = i; if (abs (a[ sel] [ col] ) < EPS) continue ; for (int i= col; i<= m; ++ i) swap (a[ sel] [ i] , a[ row] [ i] ) ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row) { double c = a[ i] [ col] / a[ row] [ col] ; for (int j= col; j<= m; ++ j) a[ i] [ j] - = a[ row] [ j] * c; } ++ row; } ans.assign (m, 0 ) ; for (int i= 0 ; i< m; ++ i) if (where[ i] ! = - 1 ) ans[ i] = a[ where[ i] ] [ m] / a[ where[ i] ] [ i] ; for (int i= 0 ; i< n; ++ i) { double sum = 0 ; for (int j= 0 ; j< m; ++ j) sum + = ans[ j] * a[ i] [ j] ; if (abs (sum - a[ i] [ m] ) > EPS) return 0 ; } for (int i= 0 ; i< m; ++ i) if (where[ i] == - 1 ) return INF; return 1 ; }

В функции поддерживаются два указателя — на текущий столбец и текущую строку .

Также заводится вектор , в котором для каждой переменной записано, в какой строке должна она получиться (иными словами, для каждого столбца записан номер строки, в которой этот столбец отличен от нуля). Этот вектор нужен, поскольку некоторые переменные могли не "определиться" в ходе решения (т.е. это независимые переменные, которым можно присвоить произвольное значение — например, в приведённой реализации это нули).

Реализация использует технику partial pivoting, производя поиск строки с максимальным по модулю элементом, и переставляя затем эту строку в позицию (хотя явную перестановку строк можно заменить обменом двух индексов в некотором массиве, на практике это не даст реального выигрыша, т.к. на обмены тратится операций).

В реализации в целях простоты текущая строка не делится на опорный элемент — так что в итоге по окончании работы алгоритма матрица становится не единичной, а диагональной (впрочем, по-видимому, деление строки на ведущий элемент позволяет несколько уменьшить возникающие погрешности).

После нахождения решения оно подставляется обратно в матрицу — чтобы проверить, имеет ли система хотя бы одно решение или нет. Если проверка найденного решения прошла успешно, то функция возвращает или — в зависимости от того, есть ли хотя бы одна независимая переменная или нет.

Асимптотика

Оценим асимптотику полученного алгоритма. Алгоритм состоит из фаз, на каждой из которых происходит:

Очевидно, первый пункт имеет меньшую асимптотику, чем второй. Заметим также, что второй пункт выполняется не более раз — столько, сколько может быть зависимых переменных в СЛАУ.

Таким образом, итоговая асимптотика алгоритма принимает вид .

При эта оценка превращается в .

Заметим, что когда СЛАУ рассматривается не в поле действительных чисел, а в поле по модулю два, то систему можно решать гораздо быстрее — об этом см. ниже в разделе "Решение СЛАУ по модулю".

Более точная оценка числа действий

Как мы уже знаем, время работы всего алгоритма фактически определяется временем, затрачиваемым на исключение текущего уравнения из остальных.

Это может происходить на каждом из шагов, при этом текущее уравнение прибавляется ко всем остальным. При прибавлении работа идёт только со столбцами, начиная с текущего. Таким образом, в сумме получается операций.

Дополнения

Ускорение алгоритма: разделение его на прямой и обратный ход

Добиться двукратного ускорения алгоритма можно, рассмотрев другую его версию, более классическую, когда алгоритм разбивается на фазы прямого и обратного хода.

В целом, в отличие от описанного выше алгоритма, можно приводить матрицу не к диагональному виду, а к треугольному виду — когда все элементы строго ниже главной диагонали равны нулю.

Система с треугольной матрицей решается тривиально — сначала из последнего уравнения сразу находится значение последней переменной, затем найденное значение подставляется в предпоследнее уравнение и находится значение предпоследней переменной, и так далее. Этот процесс и называется обратным ходом алгоритма Гаусса.

Прямой ход алгоритма Гаусса — это алгоритм, аналогичный описанному выше алгоритму Гаусса-Жордана, за одним исключением: текущая переменная исключается не из всех уравнений, а только из уравнений после текущего. В результате этого действительно получается не диагональная, а треугольная матрица.

Разница в том, что прямой ход работает быстрее алгоритма Гаусса-Жордана — поскольку в среднем он делает в два раза меньше прибавлений одного уравнения к другому. Обратный ход работает за , что в любом случае асимптотически быстрее прямого хода.

Таким образом, если , то данный алгоритм будет делать уже операций — что в два раза меньше алгоритма Гаусса-Жордана.

Решение СЛАУ по модулю

Для решения СЛАУ по модулю можно применять описанный выше алгоритм, он сохраняет свою корректность.

Разумеется, теперь становится ненужным использовать какие-то хитрые техники выбора опорного элемента — достаточно найти любой ненулевой элемент в текущем столбце.

Если модуль простой, то никаких сложностей вообще не возникает — происходящие по ходу работы алгоритма Гаусса деления не создают особых проблем.

Особенно замечателен модуль, равный двум : для него все операции с матрицей можно производить очень эффективно. Например, отнимание одной строки от другой по модулю два — это на самом деле их симметрическая разность ("xor"). Таким образом, весь алгоритм можно значительно ускорить, сжав всю матрицу в битовые маски и оперируя только ими. Приведём здесь новую реализацию основной части алгоритма Гаусса-Жордана, используя стандартный контейнер C++ "bitset":

int gauss (vector < bitset< N> > a, int n, int m, bitset< N> & ans) { vector< int > where (m, - 1 ) ; for (int col= 0 , row= 0 ; col< m && row< n; ++ col) { for (int i= row; i< n; ++ i) if (a[ i] [ col] ) { swap (a[ i] , a[ row] ) ; break ; } if (! a[ row] [ col] ) continue ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row && a[ i] [ col] ) a[ i] ^ = a[ row] ; ++ row; }

Как можно заметить, реализация стала даже немного короче, при том, что она значительно быстрее старой реализации — а именно, быстрее в раза за счёт битового сжатия. Также следует отметить, что решение систем по модулю два на практике работает очень быстро, поскольку случаи, когда от одной строки надо отнимать другую, происходят достаточно редко (на разреженных матрицах этот алгоритм может работать за время скорее порядка квадрата от размера, чем куба).

Если модуль произвольный (не обязательно простой), то всё становится несколько сложнее. Понятно, что пользуясь Китайской теоремой об остатках , мы сводим задачу с произвольным модулем только к модулям вида "степень простого". [ дальнейший текст был скрыт, т.к. это непроверенная информация — возможно, неправильный способ решения ]

Наконец, рассмотрим вопрос числа решений СЛАУ по модулю . Ответ на него достаточно прост: число решений равно , где — модуль, — число независимых переменных.

Немного о различных способах выбора опорного элемента

Как уже говорилось выше, однозначного ответа на этот вопрос нет.

Эвристика "partial pivoting", которая заключалась в поиске максимального элемента в текущем столбце, работает на практике весьма неплохо. Также оказывается, что она даёт практически тот же результат, что и "full pivoting" — когда опорный элемент ищется среди элементов целой подматрицы — начиная с текущей строки и с текущего столбца.

Но интересно отметить, что обе эти эвристики с поиском максимального элемента, фактически, очень зависят от того, насколько были промасштабированы исходные уравнения. Например, если одно из уравнений системы умножить на миллион, то это уравнение почти наверняка будет выбрано в качестве ведущего на первом же шаге. Это кажется достаточно странным, поэтому логичен переход к немного более сложной эвристике — так называемому "implicit pivoting" .

Эвристика implicit pivoting заключается в том, что элементы различных строк сравниваются так, как если бы обе строки были пронормированы таким образом, что максимальный по модулю элемент в них был бы равен единице. Для реализации этой техники надо просто поддерживать текущий максимум в каждой строке (либо поддерживать каждую строку так, чтобы максимум в ней был равен единице по модулю, но это может привести к увеличению накапливаемой погрешности).

Улучшение найденного ответа

Поскольку, несмотря на различные эвристики, алгоритм Гаусса-Жордана всё равно может приводить к большим погрешностям на специальных матрицах даже размеров порядка - .

В связи с этим, полученный алгоритмом Гаусса-Жордана ответ можно улучшить, применив к нему какой-либо простой численный метод — например, метод простой итерации.

Таким образом, решение превращается в двухшаговое: сначала выполняется алгоритм Гаусса-Жордана, затем — какой-либо численный метод, принимающий в качестве начальных данных решение, полученное на первом шаге.

Такой приём позволяет несколько расширить множество задач, решаемых алгоритмом Гаусса-Жордана с приемлемой погрешностью.

Литература

William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes: The Art of Scientific Computing
Anthony Ralston, Philip Rabinowitz. A first course in numerical analysis

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений? и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы : . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе . Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число: Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули: Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном.... Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования: (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем! (2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее. (3) К третьей строке прибавили вторую строку, умноженную на 5. (4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена . (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.

Обратный ход:

Ответ :

Пример 5: Решение : Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

Ответ :

Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).

Мы знаем, что система линейных алгебраических уравнений может:

1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.

Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Преобразования расширенной матрицы (это матрица системы - матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:

1) с троки матрицыможно переставлять местами.

2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.

3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .

4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.

5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.

В методе Гаусса элементарные преобразования не меняют решение системы уравнений.

Метод Гаусса состоит из двух этапов:

«Прямой ход» - с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:

Для этого выполним следующие действия:

1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.

2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.

3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.

«Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.

Пример.

Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).

2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.

5 шаг . Третью строку разделили на 3.

Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23) , и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:

x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1

Ответ :x 1 = –1, x 2 = 3, x 3 = 1.

Решим эту же систему по предложенному алгоритму. Получаем

4 2 –1 1
5 3 –2 2
3 2 –3 0

Разделим второе уравнение на 5, а третье – на 3. Получим:

4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0

Умножим второе и третье уравнения на 4, получим:

4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0

Вычтем из второго и третьего уравнений первое уравнение, имеем:

4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1

Разделим третье уравнение на 0,64:

4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625

Умножим третье уравнение на 0,4

4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625

Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:

4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225

Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.

х 2 = 3 и х 1 = –1.

Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.

Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.

Желаю успехов! До встречи на занятиях! Репетитор .

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

Существуют следующие элементарные преобразования:

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

Элементарные преобразования не меняют решение системы уравнений

Вернемся к нашей системе . Она практически разобрана по косточкам.

(2) Делим вторую строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Результат записываем во вторую строку:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :

А мысленный ход самих расчётов я уже рассмотрел выше.

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Пример 3

Решить систему линейных уравнений методом Гаусса

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Пример 5

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:

В данной статье метод рассматривается как способ решения Метод является аналитическим, то есть позволяет написать алгоритм решения в общем виде, а потом уже подставлять туда значения из конкретных примеров. В отличие от матричного метода или формул Крамера, при решении системы линейных уравнений методом Гаусса можно работать и с теми, что имеют решений бесконечно много. Или не имеют его вовсе.

Что значит решить методом Гаусса?

Для начала необходимо нашу систему уравнений записать в Выглядит это следующим образом. Берется система:

Коэффициенты записываются в виде таблицы, а справа отдельным столбиком - свободные члены. Столбец со свободными членами отделяется для удобства Матрица, включающая в себя этот столбец, называется расширенной.

Далее основную матрицу с коэффициентами нужно привести к верхней треугольной форме. Это основной момент решения системы методом Гаусса. Проще говоря, после определенных манипуляций матрица должна выглядеть так, чтобы в ее левой нижней части стояли одни нули:

Тогда, если записать новую матрицу опять как систему уравнений, можно заметить, что в последней строке уже содержится значение одного из корней, которое затем подставляется в уравнение выше, находится еще один корень, и так далее.

Это описание решения методом Гаусса в самых общих чертах. А что получится, если вдруг у системы нет решения? Или их бесконечно много? Чтобы ответить на эти и еще множество вопросов, необходимо рассмотреть отдельно все элементы, использующиеся при решении методом Гаусса.

Матрицы, их свойства

Никакого скрытого смысла в матрице нет. Это просто удобный способ записи данных для последующих операций с ними. Бояться их не надо даже школьникам.

Матрица всегда прямоугольная, потому что так удобнее. Даже в методе Гаусса, где все сводится к построению матрицы треугольного вида, в записи фигурирует прямоугольник, только с нулями на том месте, где нет чисел. Нули можно не записывать, но они подразумеваются.

Матрица имеет размер. Ее "ширина" - число строк (m), "длина" - число столбцов (n). Тогда размер матрицы A (для их обозначения обычно используются заглавные латинские буквы) будет обозначаться как A m×n . Если m=n, то эта матрица квадратная, и m=n - ее порядок. Соответственно, любой элемент матрицы A можно обозначить через номер его строки и столбца: a xy ; x - номер строки, изменяется , y - номер столбца, изменяется .

В - это не основной момент решения. В принципе, все операции можно выполнять непосредственно с самими уравнениями, однако запись получится куда более громоздкая, и в ней будет гораздо легче запутаться.

Определитель

Еще у матрицы есть определитель. Это очень важная характеристика. Выяснять его смысл сейчас не стоит, можно просто показать, как он вычисляется, а потом рассказать, какие свойства матрицы он определяет. Наиболее простой способ нахождения определителя - через диагонали. В матрице проводятся воображаемые диагонали; элементы, находящиеся на каждой из них, перемножаются, а затем полученные произведения складываются: диагонали с наклоном вправо - со знаком "плюс", с наклоном влево - со знаком "минус".

Крайне важно отметить, что вычислять определитель можно только у квадратной матрицы. Для прямоугольной матрицы можно сделать следующее: из количества строк и количества столбцов выбрать наименьшее (пусть это будет k), а затем в матрице произвольным образом отметить k столбцов и k строк. Элементы, находящиеся на пересечении выбранных столбцов и строк, составят новую квадратную матрицу. Если определитель такой матрицы будет числом, отличным от нуля, то назовется базисным минором первоначальной прямоугольной матрицы.

Перед тем как приступить к решению системы уравнений методом Гаусса, не мешает посчитать определитель. Если он окажется нулевым, то сразу можно говорить, что у матрицы количество решений либо бесконечно, либо их вообще нет. В таком печальном случае надо идти дальше и узнавать про ранг матрицы.

Классификация систем

Существует такое понятие, как ранг матрицы. Это максимальный порядок ее определителя, отличного от нуля (если вспомнить про базисный минор, можно сказать, что ранг матрицы - порядок базисного минора).

По тому, как обстоят дела с рангом, СЛАУ можно разделить на:

Совместные. У совместных систем ранг основной матрицы (состоящей только из коэффициентов) совпадает с рангом расширенной (со столбцом свободных членов). Такие системы имеют решение, но необязательно одно, поэтому дополнительно совместные системы делят на:
- определенные - имеющие единственное решение. В определенных системах равны ранг матрицы и количество неизвестных (или число столбцов, что есть одно и то же);
- неопределенные - с бесконечным количеством решений. Ранг матриц у таких систем меньше количества неизвестных.
Несовместные. У таких систем ранги основной и расширенной матриц не совпадают. Несовместные системы решения не имеют.

Метод Гаусса хорош тем, что позволяет в ходе решения получить либо однозначное доказательство несовместности системы (без вычисления определителей больших матриц), либо решение в общем виде для системы с бесконечным числом решений.

Элементарные преобразования

До того как приступить непосредственно к решению системы, можно сделать ее менее громоздкой и более удобной для вычислений. Это достигается за счет элементарных преобразований - таких, что их выполнение никак не меняет конечный ответ. Следует отметить, что некоторые из приведенных элементарных преобразований действительны только для матриц, исходниками которых послужили именно СЛАУ. Вот список этих преобразований:

Перестановка строк. Очевидно, что если в записи системы поменять порядок уравнений, то на решение это никак не повлияет. Следовательно, в матрице этой системы также можно менять местами строки, не забывая, конечно, про столбец свободных членов.
Умножение всех элементов строки на некоторый коэффициент. Очень полезно! С помощью него можно сократить большие числа в матрице или убрать нули. Множество решений, как обычно, не изменится, а выполнять дальнейшие операции станет удобнее. Главное, чтобы коэффициент не был равен нулю.
Удаление строк с пропорциональными коэффициентами. Это отчасти следует из предыдущего пункта. Если две или более строки в матрице имеют пропорциональные коэффициенты, то при умножении/делении одной из строк на коэффициент пропорциональности получаются две (или, опять же, более) абсолютно одинаковые строки, и можно убрать лишние, оставив только одну.
Удаление нулевой строки. Если в ходе преобразований где-то получилась строка, в которой все элементы, включая свободный член, - ноль, то такую строку можно назвать нулевой и выкинуть из матрицы.
Прибавление к элементам одной строки элементов другой (по соответствующим столбцам), умноженных на некоторый коэффициент. Самое неочевидное и самое важное преобразование из всех. На нем стоит остановиться поподробнее.

Прибавление строки, умноженной на коэффициент

Для простоты понимания стоит разобрать этот процесс по шагам. Берутся две строки из матрицы:

a 11 a 12 ... a 1n | b1

a 21 a 22 ... a 2n | b 2

Допустим, необходимо ко второй прибавить первую, умноженную на коэффициент "-2".

a" 21 = a 21 + -2×a 11

a" 22 = a 22 + -2×a 12

a" 2n = a 2n + -2×a 1n

Затем в матрице вторая строка заменяется на новую, а первая остается без изменений.

a 11 a 12 ... a 1n | b1

a" 21 a" 22 ... a" 2n | b 2

Необходимо заметить, что коэффициент умножения можно подобрать таким образом, чтобы в результате сложения двух строк один из элементов новой строки был равен нулю. Следовательно, можно получить уравнение в системе, где на одну неизвестную будет меньше. А если получить два таких уравнения, то операцию можно проделать еще раз и получить уравнение, которое будет содержать уже на две неизвестных меньше. А если каждый раз превращать в ноль один коэффициент у всех строк, что стоят ниже исходной, то можно, как по ступенькам, спуститься до самого низа матрицы и получить уравнение с одной неизвестной. Это и называется решить систему методом Гаусса.

В общем виде

Пусть существует система. Она имеет m уравнений и n корней-неизвестных. Записать ее можно следующим образом:

Из коэффициентов системы составляется основная матрица. В расширенную матрицу добавляется столбец свободных членов и для удобства отделяется чертой.

первая строка матрицы умножается на коэффициент k = (-a 21 /a 11);
первая измененная строка и вторая строка матрицы складываются;
вместо второй строки в матрицу вставляется результат сложения из предыдущего пункта;
теперь первый коэффициент в новой второй строке равен a 11 × (-a 21 /a 11) + a 21 = -a 21 + a 21 = 0.

Теперь выполняется та же серия преобразований, только участвуют первая и третья строки. Соответственно, в каждом шаге алгоритма элемент a 21 заменяется на a 31 . Потом все повторяется для a 41 , ... a m1 . В итоге получается матрица, где в строках первый элемент равен нулю. Теперь нужно забыть о строке номер один и выполнить тот же алгоритм, начиная со второй строки:

коэффициент k = (-a 32 /a 22);
с "текущей" строкой складывается вторая измененная строка;
результат сложения подставляется в третью, четвертую и так далее строки, а первая и вторая остаются неизменными;
в строках матрицы уже два первых элемента равны нулю.

Алгоритм надо повторять, пока не появится коэффициент k = (-a m,m-1 /a mm). Это значит, что в последний раз алгоритм выполнялся только для нижнего уравнения. Теперь матрица похожа на треугольник, или имеет ступенчатую форму. В нижней строчке имеется равенство a mn × x n = b m . Коэффициент и свободный член известны, и корень выражается через них: x n = b m /a mn . Полученный корень подставляется в верхнюю строку, чтобы найти x n-1 = (b m-1 - a m-1,n ×(b m /a mn))÷a m-1,n-1 . И так далее по аналогии: в каждой следующей строке находится новый корень, и, добравшись до "верха" системы, можно отыскать множество решений . Оно будет единственным.

Когда нет решений

Если в одной из матричных строк все элементы, кроме свободного члена, равны нулю, то уравнение, соответствующее этой строке, выглядит как 0 = b. Оно не имеет решения. И поскольку такое уравнение заключено в систему, то и множество решений всей системы - пустое, то есть она является вырожденной.

Когда решений бесконечное количество

Может получиться так, что в приведенной треугольной матрице нет строк с одним элементом-коэффициентом уравнения, и одним - свободным членом. Есть только такие строки, которые при переписывании имели бы вид уравнения с двумя или более переменными. Значит, у системы имеется бесконечное число решений. В таком случае ответ можно дать в виде общего решения. Как это сделать?

Все переменные в матрице делятся на базисные и свободные. Базисные - это те, которые стоят "с краю" строк в ступенчатой матрице. Остальные - свободные. В общем решении базисные переменные записываются через свободные.

Для удобства матрица сначала переписывается обратно в систему уравнений. Потом в последнем из них, там, где точно осталась только одна базисная переменная, она остается с одной стороны, а все остальное переносится в другую. Так делается для каждого уравнения с одной базисной переменной. Потом в остальные уравнения, там, где это возможно, вместо базисной переменной подставляется полученное для нее выражение. Если в результате опять появилось выражение, содержащее только одну базисную переменную, она оттуда опять выражается, и так далее, пока каждая базисная переменная не будет записана в виде выражения со свободными переменными. Это и есть общее решение СЛАУ.

Можно также найти базисное решение системы - дать свободным переменным любые значения, а потом для этого конкретного случая посчитать значения базисных переменных. Частных решений можно привести бесконечно много.

Решение на конкретных примерах

Вот система уравнений.

Для удобства лучше сразу составить ее матрицу

Известно, что при решении методом Гаусса уравнение, соответствующее первой строке, в конце преобразований останется неизменным. Поэтому выгодней будет, если левый верхний элемент матрицы будет наименьшим - тогда первые элементы остальных строк после операций обратятся в ноль. Значит, в составленной матрице выгодно будет на место первой строки поставить вторую.

вторая строка: k = (-a 21 /a 11) = (-3/1) = -3

a" 21 = a 21 + k×a 11 = 3 + (-3)×1 = 0

a" 22 = a 22 + k×a 12 = -1 + (-3)×2 = -7

a" 23 = a 23 + k×a 13 = 1 + (-3)×4 = -11

b" 2 = b 2 + k×b 1 = 12 + (-3)×12 = -24

третья строка: k = (-a 3 1 /a 11) = (-5/1) = -5

a" 3 1 = a 3 1 + k×a 11 = 5 + (-5)×1 = 0

a" 3 2 = a 3 2 + k×a 12 = 1 + (-5)×2 = -9

a" 3 3 = a 33 + k×a 13 = 2 + (-5)×4 = -18

b" 3 = b 3 + k×b 1 = 3 + (-5)×12 = -57

Теперь, чтобы не запутаться, необходимо записать матрицу с промежуточными результатами преобразований.

Очевидно, что такую матрицу можно сделать более удобной для восприятия с помощью некоторых операций. Например, из второй строки можно убрать все "минусы", умножая каждый элемент на "-1".

Стоит также заметить, что в третьей строке все элементы кратны трем. Тогда можно сократить строку на это число, умножая каждый элемент на "-1/3" (минус - заодно, чтобы убрать отрицательные значения).

Выглядит гораздо приятнее. Теперь надо оставить в покое первую строку и поработать со второй и третьей. Задача - прибавить к третьей строке вторую, умноженную на такой коэффициент, чтобы элемент a 32 стал равен нулю.

k = (-a 32 /a 22) = (-3/7) = -3/7 (если в ходе некоторых преобразований в ответе получилось не целое число, рекомендуется для соблюдения точности вычислений оставить его "как есть", в виде обыкновенной дроби, а уже потом, когда получены ответы, решать, стоит ли округлять и переводить в другую форму записи)

a" 32 = a 32 + k×a 22 = 3 + (-3/7)×7 = 3 + (-3) = 0

a" 33 = a 33 + k×a 23 = 6 + (-3/7)×11 = -9/7

b" 3 = b 3 + k×b 2 = 19 + (-3/7)×24 = -61/7

Снова записывается матрица с новыми значениями.

1	2	4	12
0	7	11	24
0	0	-9/7	-61/7

Как видно, полученная матрица уже имеет ступенчатый вид. Поэтому дальнейшие преобразования системы по методу Гаусса не требуются. Что здесь можно сделать, так это убрать из третьей строки общий коэффициент "-1/7".

Теперь все красиво. Дело за малым - записать матрицу опять в виде системы уравнений и вычислить корни

x + 2y + 4z = 12 (1)

7y + 11z = 24 (2)

Тот алгоритм, по которому сейчас будут находиться корни, называется обратным ходом в методе Гаусса. В уравнении (3) содержится значение z:

y = (24 - 11×(61/9))/7 = -65/9

И первое уравнение позволяет найти x:

x = (12 - 4z - 2y)/1 = 12 - 4×(61/9) - 2×(-65/9) = -6/9 = -2/3

Такую систему мы имеем право назвать совместной, да еще и определенной, то есть имеющей единственное решение. Ответ записывается в следующей форме:

x 1 = -2/3, y = -65/9, z = 61/9.

Пример неопределенной системы

Вариант решения определенной системы методом Гаусса разобран, теперь необходимо рассмотреть случай, если система неопределенная, то есть для нее можно найти бесконечно много решений.

х 1 + х 2 + х 3 + х 4 + х 5 = 7 (1)

3х 1 + 2х 2 + х 3 + х 4 - 3х 5 = -2 (2)

х 2 + 2х 3 + 2х 4 + 6х 5 = 23 (3)

5х 1 + 4х 2 + 3х 3 + 3х 4 - х 5 = 12 (4)

Сам вид системы уже настораживает, потому что количество неизвестных n = 5, а ранг матрицы системы уже точно меньше этого числа, потому что количество строк m = 4, то есть наибольший порядок определителя-квадрата - 4. Значит, решений существует бесконечное множество, и надо искать его общий вид. Метод Гаусса для линейных уравнений позволяет это сделать.

Сначала, как обычно, составляется расширенная матрица.

Вторая строка: коэффициент k = (-a 21 /a 11) = -3. В третьей строке первый элемент - еще до преобразований, поэтому не надо ничего трогать, надо оставить как есть. Четвертая строка: k = (-а 4 1 /а 11) = -5

Умножив элементы первой строки на каждый их коэффициентов по очереди и сложив их с нужными строками, получаем матрицу следующего вида:

Как можно видеть, вторая, третья и четвертая строки состоят из элементов, пропорциональных друг другу. Вторая и четвертая вообще одинаковые, поэтому одну из них можно убрать сразу, а оставшуюся умножить на коэффициент "-1" и получить строку номер 3. И опять из двух одинаковых строк оставить одну.

Получилась такая матрица. Пока еще не записана система, нужно здесь определить базисные переменные - стоящие при коэффициентах a 11 = 1 и a 22 = 1, и свободные - все остальные.

Во втором уравнении есть только одна базисная переменная - x 2 . Значит, ее можно выразить оттуда, записав через переменные x 3 , x 4 , x 5 , являющиеся свободными.

Подставляем полученное выражение в первое уравнение.

Получилось уравнение, в котором единственная базисная переменная - x 1 . Проделаем с ней то же, что и с x 2 .

Все базисные переменные, которых две, выражены через три свободные, теперь можно записывать ответ в общем виде.

Также можно указать одно из частных решений системы. Для таких случаев в качестве значений для свободных переменных выбирают, как правило, нули. Тогда ответом будет:

16, 23, 0, 0, 0.

Пример несовместной системы

Решение несовместных систем уравнений методом Гаусса - самое быстрое. Оно заканчивается сразу же, как только на одном из этапов получается уравнение, не имеющее решения. То есть этап с вычислением корней, достаточно долгий и муторный, отпадает. Рассматривается следующая система:

x + y - z = 0 (1)

2x - y - z = -2 (2)

4x + y - 3z = 5 (3)

Как обычно, составляется матрица:

1	1	-1	0
2	-1	-1	-2
4	1	-3	5

И приводится к ступенчатому виду:

k 1 = -2k 2 = -4

1	1	-1	0
0	-3	1	-2
0	0	0	7

После первого же преобразования в третьей строке содержится уравнение вида

не имеющее решения. Следовательно, система несовместна, и ответом будет пустое множество.

Преимущества и недостатки метода

Если выбирать, каким методом решать СЛАУ на бумаге ручкой, то метод, который был рассмотрен в этой статье, выглядит наиболее привлекательно. В элементарных преобразованиях гораздо труднее запутаться, чем в том случается, если приходится искать вручную определитель или какую-нибудь хитрую обратную матрицу. Однако, если использовать программы для работы с данными такого типа, например, электронные таблицы, то оказывается, что в таких программах уже заложены алгоритмы вычисления основных параметров матриц - определитель, миноры, обратная и и так далее. А если быть уверенным в том, что машина посчитает эти значения сама и не ошибется, целесообразней использовать уже матричный метод или формул Крамера, потому что их применение начинается и заканчивается вычислением определителей и обратными матрицами.

Применение

Поскольку решение методом Гаусса представляет из себя алгоритм, а матрица - это, фактически, двумерный массив, его можно использовать при программировании. Но поскольку статья позиционирует себя, как руководство "для чайников", следует сказать, что самое простое, куда метод можно запихнуть - это электронные таблицы, например, Excel. Опять же, всякие СЛАУ, занесенные в таблицу в виде матрицы, Excel будет рассматривать как двумерный массив. А для операций с ними существует множество приятных команд: сложение (складывать можно только матрицы одинаковых размеров!), умножение на число, перемножение матриц (также с определенными ограничениями), нахождение обратной и транспонированной матриц и, самое главное, вычисление определителя. Если это трудоемкое занятие заменить одной командой, можно гораздо быстрее определять ранг матрицы и, следовательно, устанавливать ее совместность или несовместность.